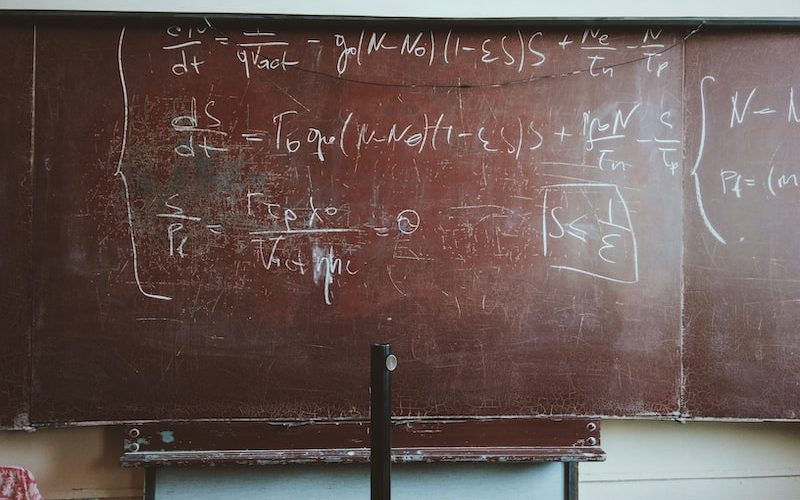Fonksiyonel analiz, matematiksel analizin bir dalıdır ve genellikle karmaşık yapılarla çalışmayı içerir. Bu disiplin, matematiksel nesneleri (ve operatörleri) vektör uzayları veya fonksiyonellik uzayları olarak ele alır. Fonksiyonel analizin temellerinden biri olan Gelfand-Naimark teoremi, bu alandaki büyük bir adımdır.
Gelfand-Naimark teoremi, 20. yüzyılın başlarında İsrail Gelfand ve Mark Naimark tarafından ortaya atıldı. Bu teorem, her C*-cebirinin birbirine izomorf olduğu bir temsilini sağlamaktadır. C*-cebirleri, soyut matematiksel objelerdir ve önemli uygulamalara sahiptir.
Bu teoremin temel fikri, bir C*-cebrinin soyut özelliklerini kullanarak onu bir Banach cebiri olarak düşünmektir. Bu şekilde, C*-cebrinin özellikleri fonksiyonel analiz prensipleriyle açıklanabilir. Gelfand-Naimark teoremi, bir C*-cebrinin bir Hilbert uzayının bağıl yansıması olduğunu gösterir.
Bu teorem, matematikte birçok uygulaması olan bir dizi sonucu beraberinde getirir. Örneğin, spektrum teorisi, Gelfand-Naimark teoreminin bir sonucudur ve matris cebirinin soyutlaştırılmasında da büyük öneme sahiptir.
Gelfand-Naimark teoremi, fonksiyonel analizin temel taşlarından biri olarak kabul edilir. Bu teorem, C*-cebrileri anlamada ve analiz etmede önemli bir rol oynar. Fonksiyonel analizde çalışan matematikçiler ve araştırmacılar için bu teorem, kavramsal bir çerçeve sunar ve daha karmaşık yapılara yönelik çalışmalarda rehberlik eder.
Gelfand-Naimark teoremi, fonksiyonel analizin temel prensiplerinden biridir ve C*-cebrilerinin soyut özelliklerini açıklamada önemli bir rol oynar. Bu teorem, matematiksel yapıların soyutlaştırılmasında kullanılır ve fonksiyonel analizi daha anlaşılır hale getirmek için kullanılan güçlü bir araçtır.
Matematikteki Gizli Hazine: Gelfand-Naimark Teoremi
Matematik, birçok insan için zorlu ve karmaşık bir konu gibi görünebilir. Ancak, matematikte bazen keşfedilen teoremler, bu disiplini daha da ilginç ve heyecan verici hale getirebilir. Bu bağlamda, matematik dünyasının gizli bir hazinesi olan Gelfand-Naimark Teoremi’nden bahsetmek istiyorum.
Gelfand-Naimark Teoremi, işlevsel analizin temel bir teoremidir ve matematiksel bilimlerde önemli bir rol oynar. Bu teorem, C*-cebraları olarak adlandırılan matematiksel yapıların tam bir karakterizasyonunu sağlar. C*-cebraları, soyut cebirsel nesnelerdir ve kuantum mekaniği, harmonik analiz ve diferansiyel denklemler gibi farklı alanlarda kullanılırlar.
Bu teorem, 20. yüzyılın başlarında İsrail Matematiksel Topluluğu’nun üyeleri olan İzrail Gelfand ve Mark Naimark tarafından formüle edildi. Teorem, bir C*-cebrasının nasıl tamamen normlu bir Banach cebiriyle eşdeğer olduğunu gösterir. Bu, bir C*-cebrasının hem cebiriksel özelliklerini hem de topolojik özelliklerini içeren bir yapıya sahip olduğunu ifade eder.
Gelfand-Naimark Teoremi, matematiksel yapıların soyutlamalarını inceleyen araştırmacılar için büyük bir ilgi odağıdır. Bu teorem, farklı matematiksel teorilerin birleştirilmesinde ve matematiğin diğer alanlarına uygulanmasında kullanışlıdır. Ayrıca, kuantum mekaniği ve fonksiyonel analiz gibi disiplinlerde de önemli bir rol oynar.
Bu teoremin keşfi, matematiğin derinliklerine inmek ve soyut düşünme becerilerini kullanmak isteyenler için büyük bir fırsat sunar. Matematikçiler, Gelfand-Naimark Teoremi’nin sonuçlarını keşfetmeye devam ediyor ve bu alanda yeni gelişmelere katkıda bulunuyorlar.
matematikteki Gelfand-Naimark Teoremi, soyut cebirsel yapıların analizini sağlayan önemli bir teoremdir. Bu teorem, matematik dünyasının gizli bir hazinesini temsil eder ve matematikçilerin araştırma ve keşif yolculuklarında önemli bir kılavuz olabilir.
Fonksiyonel Analizin Temellerini Sarsan Keşif: Gelfand-Naimark Teoremi
Gelfand-Naimark Teoremi, fonksiyonel analiz alanında önemli bir keşiftir ve temelleri sarsmıştır. Bu teorem, matematiksel yapıların soyut temsillerini sağlar ve bu sayede karmaşık analiz problemlerinin çözümünde büyük bir rol oynar. Fonksiyonel analizin temel prensiplerine dayanan bu teorem, matematiksel nesnelerin soyutlamalarını ve incelenmelerini mümkün kılar.
Gelfand-Naimark Teoremi’nin temel fikri, bir Cebirsel K-gerçeklemesi olarak adlandırılan bir özel cebirin her elemanının, bir Banach uzayındaki sınırlı doğrusal operatörlerle temsil edilebileceğidir. Bu temsil, cebirdeki işlemlerin ve ilişkilerin daha iyi anlaşılmasını ve analiz edilmesini sağlar. Teorem aynı zamanda, matematiksel yapıların farklı gösterimlerini birleştirerek, bu yapıları farklı matematiksel alanlarda inceleyebilme imkanı sunar.
Gelfand-Naimark Teoremi’nin keşfi, matematikçiler arasında büyük bir şaşkınlık yaratmıştır. Bu teoremin ortaya çıkmasıyla birlikte, cebirsel yapıların analitik yöntemlerle incelenmesi mümkün hale gelmiştir. Özellikle, spektral teori ve Banach cebirleri gibi alanlarda büyük bir ilerleme kaydedilmiştir.
Bu keşif, fonksiyonel analizin temellerini sarsmış ve matematiksel düşünceye yeni bir perspektif getirmiştir. Gelfand-Naimark Teoremi’nin önemi, matematikçiler tarafından hala aktif olarak araştırılmakta ve uygulanmaktadır. Bu teorem, matematiksel yapıların analiz edilmesinde ve daha geniş matematiksel problemlerin çözülmesinde temel bir araç olarak kabul edilmektedir.
Gelfand-Naimark Teoremi fonksiyonel analiz alanında çağdaş matematiğin temelini sarsan bir keşiftir. Bu teorem, soyut matematiksel yapıların analitik yöntemlerle incelenmesine olanak tanırken, matematikçilere yeni bir bakış açısı sunar. Gelfand-Naimark Teoremi’nin temelleri, matematiksel düşüncenin gelişiminde ve karmaşık analiz problemlerinin çözümünde önemli bir rol oynamaktadır.
Gelfand-Naimark Teoremi: Matematiksel Evreni Yeniden Tanımlamak
Matematik, evrenin derinliklerinde gizli olan bir dil gibidir. Bu dil, soyut kavramları somut ifadelerle anlamamızı sağlar. Matematikçiler, bu dili kullanarak dünyanın temel yapı taşlarını anlamaya çalışır. Bu nedenle, matematikteki keşifler ve teoremler, evrenin sırlarını çözmek için önemli adımlardır. Gelfand-Naimark Teoremi ise matematiksel evrenin yeniden tanımlanmasında devrim niteliğinde bir ilerlemedir.
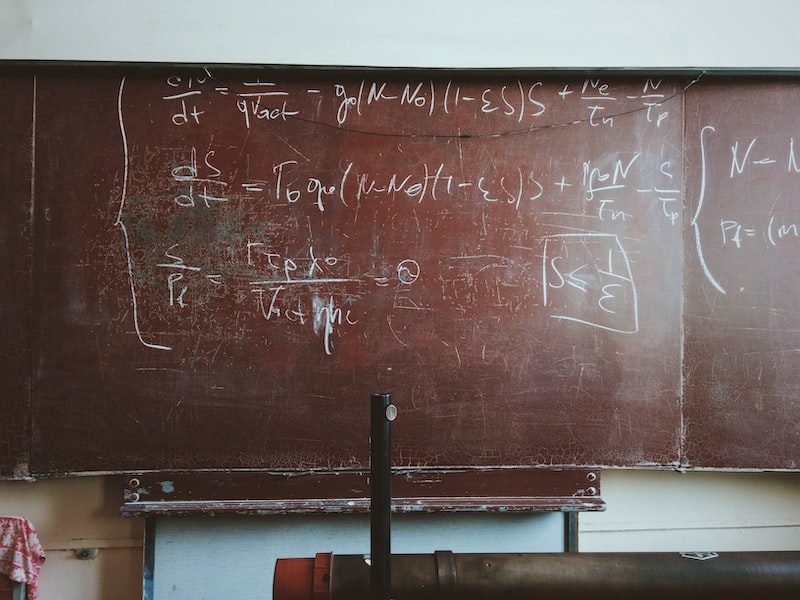
Gelfand-Naimark Teoremi, fonksiyonel analizin temel taşlarından biridir ve matematiksel fizik gibi alanlarda büyük öneme sahiptir. Bu teorem, bir C*-cebirinin soyut bir şekilde nasıl temsil edilebileceğini ortaya koymaktadır. C*-cebralar, matematiksel fizikte ve kuantum mekaniğinde kullanılan bir matematiksel yapıdır. Bu teorem, bir C*-cebrasının doğrusal operatörlerin cebirsel özelliklerini koruyarak bir Hilbert uzayı üzerinde nasıl temsil edildiğini gösterir.
Gelfand-Naimark Teoremi’nin ortaya çıkışı, matematiğin temellerinde köklü bir değişim yaratmıştır. Bu teorem sayesinde matematikçiler, soyut cebirsel yapıların somut ve fiziksel bir temsiline sahip olmuşlardır. Bu da matematiksel evrenin anlaşılmasında büyük bir ilerleme sağlamıştır.
Bu teorem, modern matematiksel düşünce için önemli sonuçlar doğurmuştur. Özellikle fonksiyonel analiz, matematiksel fizik ve kuantum alanlarında araştırmalara yeni bir bakış açısı kazandırmıştır. Gelfand-Naimark Teoremi, matematiksel düşüncede paradigmaları sarsmış ve yeni kapılar açmıştır.
Gelfand-Naimark Teoremi matematiksel evreni yeniden tanımlayan önemli bir keşiftir. Bu teorem, soyut kavramları somut ifadelerle temsil etmek için kullanılan bir araçtır. Matematiksel düşünceye yeni bir perspektif getiren bu teorem, matematikçilerin evreni daha iyi anlamalarına yardımcı olmuştur. Gelfand-Naimark Teoremi, matematiksel evrenin derinliklerine inmek isteyen herkes için heyecan verici bir keşiftir.
Bilim Dünyasında Heyecanla Karşılanan Gelfand-Naimark Teoremi
Matematik dünyasının heyecanla karşıladığı teoremlerden biri olan Gelfand-Naimark Teoremi, önemli bir yer tutmaktadır. Bu teorem, matematiksel fonksiyonların temsil edildiği alanlara ilişkin derin bir içgörü sunar. Kendine özgü yapısı ve bağlantılarıyla, matematik ve fizik gibi disiplinlerde büyük ilgi uyandırır.
Gelfand-Naimark Teoremi’nin temel ilkesi, her C* cebiri için bir C*-cebir temsili olduğunu göstermektir. Bu teorem, Banach cebiri kavramını kullanır ve bir C*-cebirini analitik fonksiyonlarla temsil etmek için spektral teorisiyle bağlantılıdır. Ayrıca, bir C*-cebirini tüm operatör cebirleriyle izomorfik hale getirebileceğimizi de gösterir.
Bu teoremin büyük bir etkisi, matematiksel fizik alanında ortaya çıkar. Özellikle, kuantum mekaniği ve kuantum alan teorisi gibi konularda kullanılır. Gelfand-Naimark Teoremi, fiziksel sistemlerin matematiksel açıklamalarında bir köprü görevi görür. Kuantum mekaniği denklemlerinin analitik ifadelerle temsil edilmesine olanak tanır ve karmaşık fiziksel sistemlerin anlaşılmasına yardımcı olur.
Bu teoremin önemi sadece matematikçiler ve fizikçiler arasında sınırlı değildir. Finans, mühendislik ve bilgisayar bilimi gibi diğer alanlarda da uygulamaları bulunmaktadır. Örneğin, finansal piyasalarda risk analizi ve portföy yönetimi gibi konularında kullanılabilir. Ayrıca, sinyal işleme ve görüntü işleme gibi alanlarda da etkili bir şekilde kullanılabilir.
Gelfand-Naimark Teoremi’nin önemi ve etkisi, matematik ve fen bilimleri topluluğunda büyük bir ilgi uyandırmıştır. Bu teorem, matematiksel yapıların temsil edilmesi ve anlaşılmasında büyük bir adımdır. Matematikçiler ve fizikçiler, bu teoremin sonuçları üzerinde çalışarak daha derinlemesine anlayışlar elde etmek için çaba göstermektedirler. Gelfand-Naimark Teoremi’nin keşfi, matematiğin evriminde bir dönüm noktası olarak kabul edilir ve hala aktif bir araştırma konusudur.
Gelfand-Naimark Teoremi, matematik ve fizik dünyasında büyük bir heyecanla karşılanan bir teoremdir. Matematiksel fonksiyonların temsil edildiği alanların analitik açıklamalarını sağlar ve birçok disiplinde uygulanabilir. Bu teorem, matematiksel yapıların temsili ve anlaşılmasında derin bir içgörü sunar ve bilim insanları arasında aktif bir araştırma konusu olarak devam etmektedir.