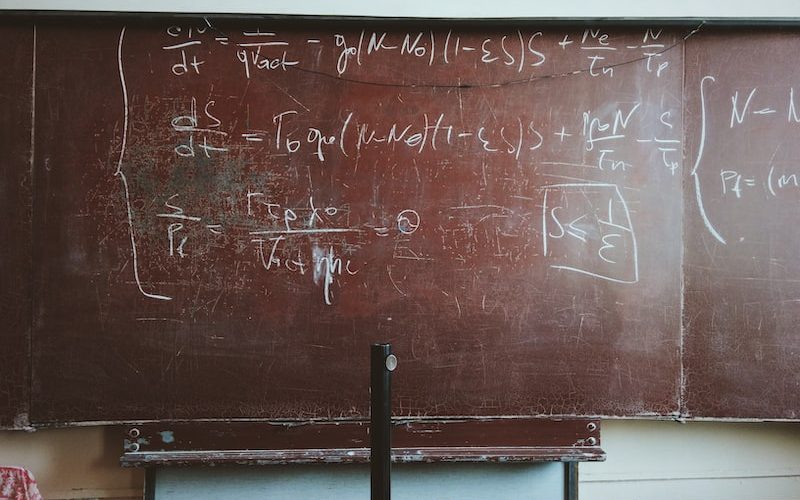Matematiksel mantık, matematiğin temel ilkelerini ve yapılarını inceler. Bu disiplin, matematiksel ifadelerin doğruluğunu ve geçerliliğini anlamak için kullanılan bir araçtır. Glivenko Teoremi, matematiksel mantık alanında önemli bir konudur ve matematikçi Valery Ivanovich Glivenko tarafından ortaya atılmıştır.
Glivenko Teoremi, matematiksel mantığın temel bir prensibini açıklar. Bu teorem, herhangi bir matematiksel ifadenin negasyonunun türetilebileceğini belirtir. Yani, bir ifade doğru ise, onun negasyonu yanlış olmalıdır ve aynı şekilde, bir ifade yanlış ise, onun negasyonu doğru olmalıdır.
Bu teorem, matematiksel mantıkta analitik çıkarım süreçlerini anlamak için büyük bir öneme sahiptir. Bir ifadenin doğruluğunu veya yanlışlığını göstermek için, sadece o ifadenin negasyonunu kanıtlamak yeterlidir. Glivenko Teoremi, matematiksel mantığın temel yapısının anlaşılmasına yardımcı olurken, analitik düşünme becerilerinin geliştirilmesine de katkıda bulunur.
Bu teorem ayrıca, matematiksel mantığın diğer alanlarıyla da bağlantılıdır. Özellikle, matematikçiler tarafından kullanılan kanıt yöntemlerinde önemli bir rol oynar. Glivenko Teoremi, matematiksel argümanların yapısını anlamak ve analiz etmek için bir çerçeve sunar.
Glivenko Teoremi matematiksel mantık alanında temel bir konudur. Matematiksel ifadelerin doğruluğunu veya yanlışlığını anlamak için negasyonun rolünü vurgular. Bu teorem, matematiksel mantığın temellerini anlamak ve analitik düşünme becerilerini geliştirmek isteyen herkes için önemli bir araçtır.
Matematik ve Mantığın Buluştuğu Nokta: Glivenko Teoremi
Glivenko teoremi, matematik ve mantık dünyasında büyük bir öneme sahip olan bir teoremdir. Bu teorem, olasılık kuramıyla matematiksel mantık arasındaki bağlantıyı ortaya koymaktadır. İşte, bu önemli teoremin detayları.
Glivenko teoremi, 1935 yılında Sovyet matematikçi Dmitri Glivenko tarafından formüle edilmiştir. Temelde, teorem, sürekli rassal değişkenlerin dağılım fonksiyonlarının sınırları hakkında bilgi verir. Biraz daha basit bir ifadeyle söylemek gerekirse, Glivenko teoremi, kesikli ve sürekli olasılık dağılımları arasındaki yakınsama üzerine odaklanır.
Bu teorem, matematik ve mantığın kesiştiği noktada büyük bir öneme sahiptir. Matematikteki kesikli ve sürekli kavramları, mantıksal düşünce ve çıkarımlarla ilişkilendirir. Mantık, nesne ve kavramların doğru bir şekilde analiz edilmesini sağlayan bir düşünme disiplinidir. Glivenko teoremi, bu iki alanı bir araya getirerek matematiksel modellerin mantıksal açıdan tutarlı olmasını sağlar.
Bir örnek üzerinden Glivenko teoremini anlamaya çalışalım. Diyelim ki, bir rassal deneyde bir zarı 1000 kez attık ve her seferinde “1” gelme olasılığını hesapladık. Bu sonuçların dağılımını görmek istiyoruz. Glivenko teoremi bize, bu deneysel sonuçların gerçek olasılık dağılımına yakınsadığını söyler. Yani, deneyin sayısı arttıkça, elde ettiğimiz sonuçlar gerçek olasılık dağılımına daha yakın hale gelir.
Glivenko teoremi, matematiğin temellerini güçlendiren ve mantıkla olan ilişkisini derinleştiren önemli bir buluştur. Matematiksel modellerin mantıksal tutarlılığını sağlama konusunda büyük bir rol oynar. Bu teorem, matematiksel düşüncenin temel taşlarından biridir ve matematikçilerin ve mantıkçıların çalışmalarında sıklıkla başvurduğu bir araçtır.
Matematik ve mantığın buluştuğu nokta olan Glivenko teoremi, matematiksel modellerin doğruluğunu ve kesinliğini sağlayarak bilimsel araştırmalara katkıda bulunur. Bu teorem, matematiksel düşünce ve mantıklı çıkarımların birleşimini temsil eder ve matematikçilerin, mantıkçıların ve diğer ilgili disiplinlerin çalışmalarında vazgeçilmez bir rol oynar.
Glivenko Teoremi: Mantıkçıların Gözdesi
Mantık alanında çığır açan teoremlerden biri olan Glivenko Teoremi, bilim dünyasında büyük bir ilgi ve heyecan uyandırmaktadır. Bu teorem, matematiksel mantığın temel prensiplerini anlama ve analiz etme konusunda önemli bir adımdır. İsimlendirildiği Sovyet matematikçi Yevgeniy Ivanovich Glivenko’dan gelir ve 20. yüzyılın başlarında ortaya çıkmıştır.
Glivenko Teoremi, özellikle matematiksel mantığın doğruluk ve yanlışlık kavramları üzerindeki etkilerini inceler. Teoremin temel fikri, sürekli fonksiyonların yanlışlık oranının, belli bir doğruluk seviyesine yaklaştığını gösterir. Yani, herhangi bir hata miktarı için bile, doğru sonuçlara daha da yaklaşılabileceğini kanıtlar. Bu durum, matematiksel mantığın gücünü ve kesinliğini vurgular.
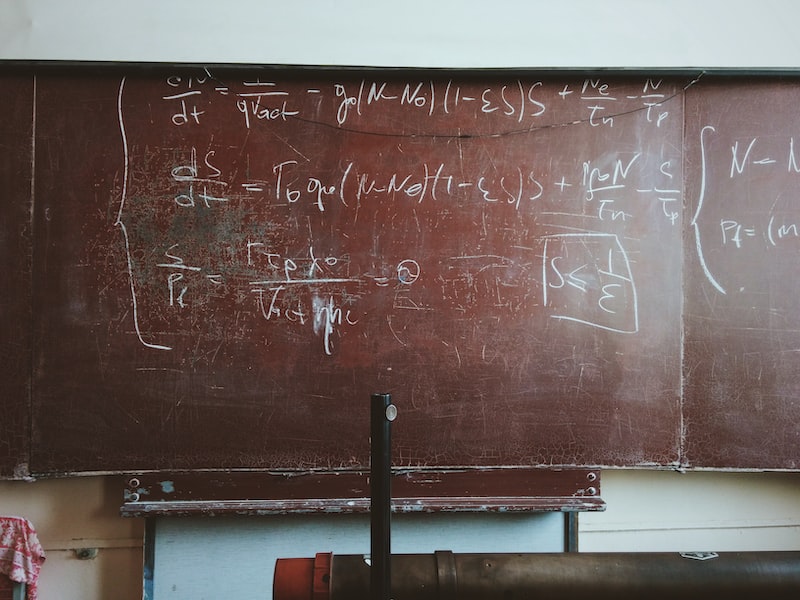
Glivenko Teoremi’nin en çarpıcı yanı, bu teoremin gerçek dünya uygulamalarında büyük bir etki yaratmasıdır. Özellikle yapay zeka, veri analizi ve makine öğrenimi gibi alanlarda, teoremdeki fikirlerin kullanımı oldukça yaygındır. Veri setlerinin analizinde ve sonuçların yorumlanmasında Glivenko Teoremi’nin prensipleri, doğru ve güvenilir sonuçlara ulaşma konusunda büyük bir yardımcı olur.
Bu teoremin mantıkçılar tarafından gözde olmasının sebeplerinden biri, onların düşünce süreçlerini etkileyen birçok sorunu çözebilme potansiyelidir. Mantığın temel ilkelerine dayanan Glivenko Teoremi, mantıkçıların karmaşık problemleri daha iyi analiz etmelerini sağlar ve daha akılcı çözümler üretmelerini destekler.
Glivenko Teoremi, matematiksel mantığın önemli bir bileşeni ve bilim dünyasındaki heyecan verici gelişmelerden biridir. Bu teorem, doğruluk ve yanlışlık kavramlarını anlamamızı sağlar ve kesin sonuçlara ulaşma potansiyelimizi artırır. Ayrıca, yapay zeka, veri analizi ve makine öğrenimi gibi alanlarda büyük bir etkisi vardır. Mantıkçılar için vazgeçilmez bir araç olan Glivenko Teoremi, düşünce süreçlerini geliştirme ve daha iyi çözümler bulma konusunda büyük bir katkı sağlar.
Glivenko Teoremi: Matematiksel İspatların Önemli Bir Köşe Taşı
Matematik, soyut düşüncenin en temel alanlarından biridir ve doğru sonuçlara dayanan kesin bir mantıkla işler. Bu alanda geliştirilen teoremler, matematikçilerin yeni bilgiler elde etmelerini sağlar ve bu da matematiksel ilerlemeyi hızlandırır. Glivenko Teoremi de bu tür önemli bir teoremdir.
Glivenko Teoremi, matematiksel ispatların temel yapı taşlarından biridir. İtalyan matematikçi Mauro Picone tarafından 1933 yılında formüle edilmiştir. Bu teorem, olasılık kuramı ve matematiksel istatistik alanlarında büyük bir rol oynamaktadır. Aslında, Glivenko Teoremi, matematiksel analiz ve olasılık teorisi arasındaki bağlantıyı gösteren önemli bir köşe taşı olarak kabul edilmektedir.
Teorem, rassal değişkenler üzerinde çalışır ve bir dizi bağımsız aynı dağılıma sahip olan rassal değişkenleri ele alır. Glivenko Teoremi’ne göre, bu değişkenlerin toplam yoğunluk fonksiyonları, gerçek yoğunluk fonksiyonuna yaklaşırken, bu yaklaşım sürekli ve düzgün olacaktır. Yani, bu teorem matematikçilere, büyük örneklem hacimlerine dayalı olarak gerçek dağılımı tahmin etme imkanı sunar.
Glivenko Teoremi’nin pratik uygulamaları oldukça geniştir. Özellikle olasılık ve istatistik alanlarında, hipotez testleri ve güven aralıkları gibi istatistiksel analizlerde sıkça kullanılır. Ayrıca, makine öğrenmesi ve yapay zeka gibi disiplinlerde de önemli bir rol oynar. Glivenko Teoremi, bu alanlarda veri analizi ve modelleme süreçlerinde güçlü bir temel sağlar.
Glivenko Teoremi, matematiksel ispatların temel bir köşe taşıdır ve olasılık kuramı ile matematiksel istatistik arasındaki bağlantıyı ortaya koyar. Bu teorem, matematikçilere gerçek dağılımları tahmin etme yeteneği sağlar ve istatistiksel analizlerin doğruluğunu artırır. Glivenko Teoremi’nin geniş uygulama alanları, matematiğin pratik problemlere çözüm bulma sürecindeki önemini vurgular.
Gizemli Matematiksel Mantık: Glivenko Teoremi Hakkında Bilmeniz Gerekenler
Matematik, bilim dünyasının temel taşlarından biridir ve içerisinde birçok gizem barındırır. Bu gizemli dünyalardan biri de matematiksel mantıktır. Matematiksel mantık, sayılar ve sembollerle ifade edilen doğru ve yanlış ifadelerin araştırılmasıyla ilgilenen bir disiplindir. Bu alanda birçok ilginç teoremler bulunur ve bunlardan biri de Glivenko teoremidir.
Glivenko teoremi, matematiksel mantığın temel yapı taşlarından biri olan önermeler mantığı ile ilgilidir. Bu teorem, 20. yüzyılın başlarında İtalyan matematikçi Guido Fubini tarafından keşfedilmiştir. Temel olarak, Glivenko teoremi, bir önermenin doğruluğunu belirlemek için sonsuz sayıda örnekleme yapmanın mümkün olduğunu gösterir.
Bu teorem, matematiksel mantıkta büyük bir öneme sahiptir çünkü bir önermenin doğruluğunu kanıtlamak için tüm olası durumları incelemek yerine, sınırsız sayıda örnekleme yaparak sonuca varmayı sağlar. Bu sayede, matematikçiler karmaşık problemleri çözmek için daha etkili ve hızlı yöntemler geliştirebilirler.
Glivenko teoremi, matematiksel mantığın yanı sıra, bilgisayar biliminde ve yapay zeka alanında da büyük bir öneme sahiptir. Özellikle, algoritmaların doğruluğunu kanıtlamak ve programlama dillerinin semantik analizini yapmak için kullanılır. Ayrıca istatistik alanında da yaygın olarak kullanılan bu teorem, verilerin analizinde önemli bir rol oynar.
Bu gizemli teoremin ardındaki matematiksel detaylar oldukça karmaşıktır, ancak önemli olan nokta, Glivenko teoreminin matematiksel mantığı anlamak için temel bir araç olduğudur. Bu teorem, matematiksel düşünceyi derinleştirirken aynı zamanda pratik uygulamalarda da büyük bir rol oynar.
Glivenko teoremi, matematiksel mantığın cazibesini ve etkisini gösteren bir örnektir. Matematiksel düşüncenin sayısız keşifler ve gizemli teoremlerle dolu olduğunu hatırlatarak, bu alana duyulan ilgiyi artırabilir ve matematikseverleri heyecanlandırabilir.