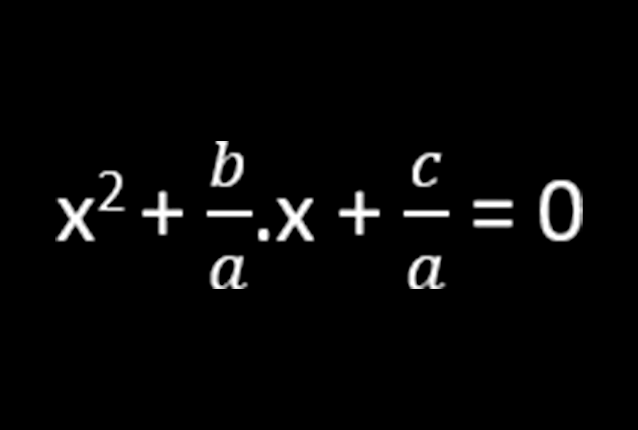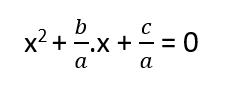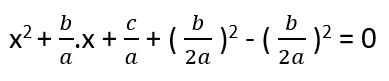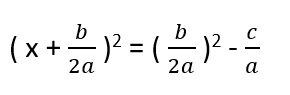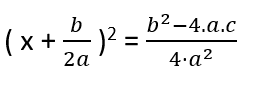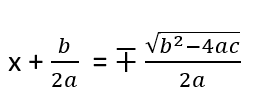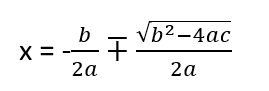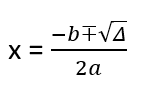2. Dereceden denklemlerin genel gösterimi olarak kullandığımız
İKİNCİ DERECEDEN DENKLEMLERDE KÖKLERİ İSPAT
ax2 + b.x + c = 0 ifadesinin öncelikle köklerini bulalım.
Öncelikle her iki tarafı da a ‘ya bölelim: ( bu durumda a’nın sıfırdan farklı bir sayı olması gerekir. )
Peki matematikte kafamıza göre her iki tarafı da bir şey ile çarpabiliyor muyuz? Örneğin ( x-1 ) = 0 ifadesinde her iki tarafı da ( x-2 ) ile çarparsak ( x-1 ) . ( x-2 ) = 0 eşitliğini buluyoruz. En baştaki denklemde x sadece 1 ‘e eşit idi ancak şimdi x hem 1 ‘de hemde 2 ‘ye eşit oldu.
Bu sorunun cevabı x hem 1 hemde 2 ‘ye eşit değildir. x değeri 1 yada 2 ‘ye eşittir. Yani ya 1 yada 2 sayısına eşit. Burada bir yanlışlık doğmuyor.
Elimizdeki denkleme dönecek olursak şimdi yapmamız gereken şey bir tam kare ifade oluşturmaya çalışmak olacaktır. Matematikte genelde ispatlarda elimizde böyle bir terim varsa o iki terime eklendiğinde tam kare yapacak bir ifade bulunur. Daha sonra o ifade denkleme eklenir ve çıkartılır. Matematikteki küçük oyunlardan biridir. Bizde ilk iki ifadeyi tam kare yapmak için denkleme b/2a ‘nın karesini ekleyip çıkaralım.
Yukarıda eşitliğin sağ tarafına baktığımızda payda 0 dan büyük bir sayı. Denklemin sol tarafında bir tam kare sayı olduğundan denklemin sağ tarafı da 0 veya 0 dan büyük olmak zorundadır. Paydamız pozitif olduğuna göre payın da pozitif olması gerekir. Yani b2 – 4.a.c ‘nin ( yani delta yada diskriminant ‘ın ) 0 dan küçük bir değere eşit olmaması gerekir. Diskriminantımızın 0 dan küçük olduğu değerlerde denklemin kökü yoktur. Demek ki diskriminant 0 dan büyük veya eşit olmak zorunda. Soldaki ifade bir tam kare ifade olduğundan + veya – şeklinde çıkabilir.
Şimdi her iki tarafın da karekökünü alalım: