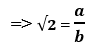Kök iki neden rasyonel değildir? √2 Gibi irrasyonel sayıların rasyonel olmadığının birçok ispatı vardır. Bu yazımızda iki farklı ispatına bakacağız. Kök iki neden rasyonel değildir?
Genelde Kullanılan 1. İspat Yöntemi:
√2 ‘Nin rasyonel olmadığını ispatlamak için önce √2‘yi bir rasyonel sayı olarak kabul edelim.
Her iki tarafında kareleri alındığında;
=> a2 = 2.b2
Denkleme göre a2 çift bir sayı. a2 çift olduğuna göre a ‘da çift olmak zorundadır. a = 2k diyelim;
=> 4.k2 = 2.b2
=> 2.k2 = b2
b2 ‘yi 2.k2 gibi çift bir sayı bulduk. Bu durumda b ‘de çift olmak zorundadır.
En başta a ve b sayılarına aralarında asal demiştik. √2‘Yi rasyonel kabul ettiğimizde a ve b sayıları çift oluyor ve bir çelişki çıkıyor. Dolayısıyla √2 rasyonel bir sayı değildir. Bu ispat yöntemiyle √7, √5 … gibi irrasyonel sayıların da rasyonel olmadığı a2 tek ise a da tek olmalı şeklinde ispatlanabilir.
2. İspat Yöntemi:
Tekrar başta bulduğumuz eşitliğe dönelim;
a2 = 2.b2
a2 çift olduğundan a ‘da çift olmak zorundaydı. a = 2.k dersek a2 = 4.k2 eşitliği çıkıyor. Yani eşitliğin sol tarafındaki a2 ifadesi 4 ‘e tam bölünen bir ifadedir. a ve b aralarında asal olmak zorunda olduğundan b tek bir sayı olmalıdır. Dolayısıyla b2 ‘de tek bir sayıdır. Eşitliğin sağ tarafındaki a2 ifadesi 4 ‘e tam bölünüyor ancak eşitliğin sol tarafındaki 2.b2 ifadesi 4 ‘e bölünemiyor. Sadece 2 ‘ye bölünebiliyor. Yine bir çelişki elde etmiş olduk.
Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.