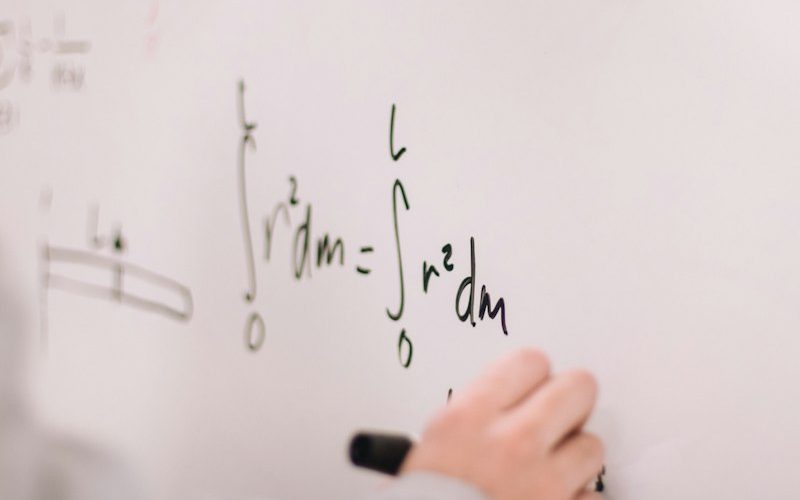L’Hôpital Kuralı, türevlerin hesaplanmasıyla ilgili karmaşık problemleri çözmek için kullanılan bir matematiksel yöntemdir. Bu kural, limitlerdeki belirsizlik durumlarında uygulanır ve orantısızlık durumlarını çözümlemeye yardımcı olur.
L’Hôpital Kuralı, bir fonksiyonun limitini hesaplarken, hem paydanın hem de payın ayrı ayrı limitlerini alarak sonucu elde etme prensibine dayanır. Eğer pay ve payda fonksiyonları belirli bir değerde sınırsız veya sıfıra yakın olduğunda, L’Hôpital Kuralı devreye girer ve bu sorunu çözmek için daha kolay bir yaklaşım sunar.
Bu kuralın ana fikri şu şekildedir: Eğer iki fonksiyonun türevleri belirli bir değerde aynıysa ve bu fonksiyonlar o değerde sınırsız veya sıfıra yakın değerlere sahipse, bu durumdaki limitin değeri, iki fonksiyonun türevlerinin oranının limitinin değeriyle aynıdır.
Örneğin, bir fonksiyonun limitini hesaplarken pay ve payda fonksiyonları sırasıyla sıfıra yaklaşıyorsa ve bu fonksiyonların türevleri belirli bir değerde eşit ise, L’Hôpital Kuralı kullanılarak limit hesaplanabilir. Bu yöntem, birçok karmaşık problemin çözümünde büyük kolaylık sağlar ve analizle ilgilenen matematikçiler için önemli bir araçtır.
L’Hôpital Kuralı’nın temel prensiplerini anlamak, türevlerin hesaplanmasıyla ilgili zorlu problemleri daha etkili bir şekilde çözmek için büyük bir avantaj sağlar. Bu kuralın kullanımıyla, limitlerdeki belirsizlik durumlarını ortadan kaldırarak daha kesin sonuçlara ulaşabilirsiniz. L’Hôpital Kuralı, matematiksel analizin temel taşlarından biri olarak kabul edilir ve birçok matematiksel disiplinde sıklıkla kullanılır.
Matematik Dünyasının Gizemli İlkesi: L’Hôpital Kuralı
Matematik, evrenin derinliklerindeki sırları çözmek için kullanılan bir dil olarak kabul edilir. Bu dildeki en gizemli ve ilginç ilke, L’Hôpital Kuralıdır. L’Hôpital Kuralı, belirsizlik durumlarında limit hesaplarken kullanılan bir yöntemdir.
Belirsizlik durumları, matematiksel ifadelerde sıkça karşımıza çıkar. Örneğin, bir fonksiyonun limitini hesaplamak istediğimizde, bazen 0/0 veya ∞/∞ gibi belirsiz ifadelere ulaşabiliriz. İşte tam bu noktada L’Hôpital Kuralı devreye girer.
L’Hôpital Kuralı’nın temel prensibi, belirsizlik durumundaki bir ifadeyi daha basit bir forma dönüştürmektir. Bu kuralı uygulamak için, paydanın ve payın türetilmesi gerekmektedir. Ardından, elde edilen yeni ifadeyi tekrarlimite tabi tutarak sonucu bulabiliriz.
Bu matematiksel hile, pek çok zorlu problemin çözümünde büyük kolaylık sağlar. Ancak, doğru sonuçlara ulaşmak için dikkatli olunması gereken bazı noktalar vardır. Öncelikle, belirsizliğin sağ ve sol limitlerinin ayrı ayrı hesaplanması gerekmektedir. Bunun yanı sıra, L’Hôpital Kuralı’nın uygulanabilmesi için ifadenin belirsizliğe indirgenmesi gerekmektedir.
L’Hôpital Kuralı, matematik dünyasında geniş bir kullanım alanına sahiptir. Özellikle diferansiyel hesaplamalarda ve analitik fonksiyonların çözümünde sıkça başvurulan bir yöntemdir. Ayrıca, trigonometrik fonksiyonların limitini hesaplarken de etkili sonuçlar verir.
L’Hôpital Kuralı matematik dünyasının gizemli prensiplerinden biridir. Belirsizlik durumlarında limiti hesaplarken, bu kuralı kullanarak karmaşık problemleri basitleştirebilir ve doğru sonuçlara ulaşabiliriz. Matematiğin derinliklerinde kaybolmadan, L’Hôpital Kuralı’nı keşfetmek, matematiksel anlayışımızı ve yeteneklerimizi geliştirmek için önemli bir adımdır.
Sonsuzlukta Sınırını Aşan Matematiksel İlke: L’Hôpital Kuralı
Matematik, insan zihninin sınırlarını zorlayan bir bilim dalıdır. Sonsuzluk kavramı ise matematikte en ilginç ve aynı zamanda karmaşık konulardan biridir. İşte bu noktada L’Hôpital kuralı devreye girer. L’Hôpital kuralı, belirsizlik durumlarında türevleri kullanarak limit problemlerini çözen bir yöntemdir.
L’Hôpital kuralının adı, 17. yüzyıl Fransız matematikçi Guillaume François Antoine de l’Hôpital’den gelmektedir. Bu kural, bir fonksiyonun limitini bulmak için kullanılırken, payda ve paydada yer alan fonksiyonlar ayrı ayrı türevlenir. Ardından elde edilen yeni ifadelerin limiti hesaplanır. Eğer limit hala belirsizlik gösteriyorsa, yeni ifadeler tekrar türevlenir. Bu işlem, belirsizlik ortadan kalkana kadar tekrarlanır.
L’Hôpital kuralının gücü, sonsuzlukta sınırını aşabilmesindedir. Özellikle rasyonel fonksiyonların limitlerini hesaplarken sıklıkla kullanılır. Bu kural sayesinde, bazen karmaşık limit problemleri kolayca çözülebilir. Ayrıca trigonometrik fonksiyonlar, üstel fonksiyonlar ve logaritmalar gibi diğer fonksiyonlarla da kullanılabilir.
L’Hôpital kuralı, matematiksel analizin temel taşlarından biridir. Öğrencilerin ve matematikçilerin limit hesaplamalarını daha kolay ve doğru bir şekilde yapmalarına yardımcı olur. Bu kuralın anlaşılması ve uygulanması, matematik bilimine olan ilgiyi artırabilir.
Sonsuzlukta sınırını aşan matematiksel ilke olan L’Hôpital kuralı, matematik dünyasında büyük bir etkiye sahiptir. Belirsizlik durumlarına pratik bir çözüm sunarak matematikçilere yeni perspektifler kazandırır. Limit problemlerinin çözümünde güvenilir bir araç olarak kullanılabilen bu kural, matematiğin evrenindeki engelleri aşmaya yardımcı olur.
Zorlu Limit Problemlerini Çözmek İçin Bir Silah: L’Hôpital Kuralı
Limit problemleri matematiksel analizin temel kavramlarından biridir ve çoğu zaman karmaşık hale gelebilir. Neyse ki, limit problemlerinin zorluklarını aşmada L’Hôpital kuralı gibi güçlü bir araç bulunmaktadır. Bu kural, belirsizlik halinde olan limit ifadelerini daha basit bir hale getirerek çözmeyi mümkün kılar.
L’Hôpital kuralı, ilk olarak Fransız matematikçi Guillaume de l’Hôpital tarafından 17. yüzyılda formüle edilmiştir. Temel olarak, bir fonksiyonun limiti belirsizlik verdiğinde, bu kuralı kullanarak orantılı türevlerini alırız. Bu sayede limit problemlerini daha anlaşılır ve çözülebilir hale getirebiliriz.
Kuralın uygulanması oldukça basittir. İlk adım, belirsizlik içeren ifadeyi elde ederiz. Daha sonra, sayıcı ve paydanın türevlerini ayrı ayrı alırız. Eğer bu türevler bağımsız değişkene göre sıfıra giden bir şekilde yaklaşıyorsa, orijinal limit problemini çözebilmek için bu türevleri birbirine böleriz. Bu işlem ile genellikle daha basit bir limit ifadesine ulaşırız.
L’Hôpital kuralı, sinüs, kosinüs, üstel ve logaritmik fonksiyonlar gibi birçok farklı matematiksel ifadeye uygulanabilir. Limit problemlerini çözmek için çok değerli bir araçtır çünkü bazen diğer yöntemlerle zorlu hale gelen problemlere kolayca uygulanabilir.
L’Hôpital kuralı, zorlu limit problemlerinin üstesinden gelmek için güçlü bir silahtır. Matematiksel analizdeki birçok alanda kullanılır ve karmaşık ifadeleri daha anlaşılır hale getirmeyi sağlar. Bu kuralın doğru bir şekilde uygulanması, limitlerin kesin değerlerini bulmada büyük bir yardımcıdır ve matematiksel araştırmalarda önemli bir rol oynar.
Matematikteki Kazanan El: L’Hôpital Kuralıyla Limitlerde Zafer
Matematik, bazıları için karmaşık ve zor bir konu olarak algılansa da, onunla derinlemesine ilgilenenler için büyüleyici bir zeka oyunudur. Matematiksel problemleri çözerken, bazen sınırlarla karşılaşırız ve bu noktada L’Hôpital kuralı devreye girer. Bu makalede, L’Hôpital kuralının matematikteki kazanan el olduğunu keşfedeceksiniz.
L’Hôpital kuralı, limit hesaplamalarında kullanılan bir yöntemdir. Özellikle belirsizlik durumlarında, yani paydası sıfır olan ve paydası da sıfır olmayan ifadelerde limit bulmamız gerektiğinde bize yardımcı olur. Bu kural, Guillaume de l’Hôpital tarafından geliştirilmiş ve matematik dünyasında büyük bir etki yaratmıştır.
Bu kuralın temel mantığı, belirsizlik durumlarında orantılılık ilişkisini kullanmaktır. Eğer bir fonksiyonun hem paydası hem de paydasının türevidi sıfıra yakınsıyorsa, bu durumda L’Hôpital kuralı devreye girerek limitin değerini bulmamızı sağlar. Kısacası, bu kural, sınırlarda zafer kazanmamızı sağlayan bir matematiksel silahtır.
L’Hôpital kuralı, matematikteki çeşitli alanlarda büyük öneme sahiptir. Özellikle diferansiyel hesaplamalarda, türevin tanımını kullanmadan limitleri hesaplama imkanı sunar. Bu sayede daha karmaşık fonksiyonları inceleyebilir ve analiz edebiliriz. Ayrıca, trigonometrik fonksiyonlar, üstel fonksiyonlar ve logaritmalar gibi çeşitli matematiksel ifadelerde L’Hôpital kuralıyla limitlerin değerini bulabiliriz.
Matematikteki kazanan el genellikle çözümün özgünlüğü ve basitliğiyle belirlenir. L’Hôpital kuralı, bu iki özelliği bir araya getirerek limit hesaplamalarında zafer kazanmamızı sağlar. Karmaşık problemleri daha anlaşılır hale getirirken, aynı zamanda matematiksel zekâ ve kavrayışımızı da geliştirir.
L’Hôpital kuralı matematikteki sınırlarda zaferimizi temsil eder. Belirsizlik durumlarında bize yol gösteren bu kural, limit hesaplamalarında büyük bir yardımcıdır. Matematik dünyasında önemli bir yere sahip olan L’Hôpital kuralı, basitliği ve etkinliğiyle matematikseverlerin favori silahı haline gelmiştir.