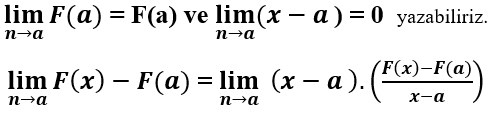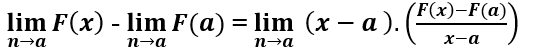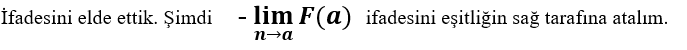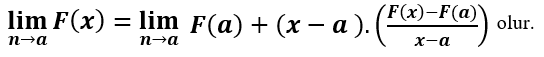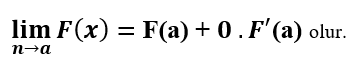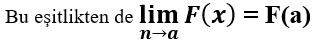“Bir fonksiyon x = a noktasında türevlenebiliyorsa süreklidir.” teoreminin ispatını yapacağız. Türevlenebiliyorsa süreklidir.
İspat:
Bir fonksiyonun sürekli olması için 3 şart vardı;
1) Fonksiyon o noktada tanımlı olmalıdır.
2) Fonksiyonun o noktadaki sağdan ve soldan limit değeri birbirine eşit olmalıdır.
3) Fonksiyonun o noktadaki fonksiyon değeri ile limit değeri birbirine eşit olmalıdır.
F(x) fonksiyonu x = a noktasında türevlenebildiğine göre o noktada tanımlıdır ve yığılma noktası a’dır.
(Yani o noktadaki sağdan ve soldan limiti birbirine eşittir.) Bu durumda F(x) fonksiyonunun x = a noktasındaki fonksiyon değeri ile limit değerinin birbirine eşit olduğunu göstermemiz yeterli olacaktır.
Yazabiliriz. (Türevin tanımından.)
Ayrıca;
Eşitliğini yazabiliriz. Gerekli sadeleştirmeler yapıldığında eşitlik sağlanıyor.
Şimdi eşitliğin sol tarafında bulunan limiti parçalayalım;
Sağ taraftaki eşitliği toplama işaretinin olduğu yerden ayırırsak;
Bu durumda yeni eşitliğimiz;
y = F(x) fonksiyonunun x = a noktasında fonksiyon değeri limit değerine eşit olduğundan süreklidir.
Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.