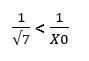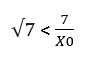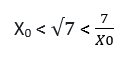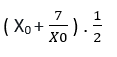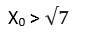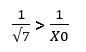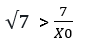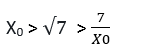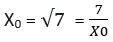Köklü sayıları nasıl hesaplıyoruz? Teknoloji hayatımızın her alanında bize büyük yardımlarda bulunuyor. Peki hesap makinelerinin √2 yazıldığında karşımıza aniden 1,414214 sayısını aniden nasıl çıkardığını hiç düşündük mü? köklü sayıları nasıl hesaplıyoruz? Köklü sayıların asıl değeri nasıl bulunur?
Hesap makinelerine tüm köklü ifadelerin karşılığı verilip bize mi sunuluyor?
Tabiki hayır hesap makinelerine √2 yazdığımız an bir algoritma yardımı ile bize 5 veya 6 adımda hızlı bir hesap yaparak saniyeler içinde köklü ifadenin değerini veriyorlar.
Bu yazıda bu algoritmayı ve bu algoritmanın nasıl doğru çıktığını inceleyeceğiz.
Bu yöntem yaklaşık 4000 yıl önce Babiller tarafından bulunmuştur.
İlk olarak ‘dan büyük herhangi bir sayı seçmemiz gerekiyor. Bu sayıya X0 diyelim.
Yukarıdaki denklemde Xn yerine X0, X1, X2 … gibi sayılar geldiğinde her seferinde çıkan sonuç belirli bir sayıya yaklaşacak.
n = 0‘dan başlayıp sabit bir sayı gelene kadar algoritma kendini tekrar etmeli. Bir örnek yapalım.
Köklü Sayıları Nasıl Hesaplıyoruz?
=>√7 sayısının hesap makinesindeki değeri olan 2,645751 sayısını 4000 yıl önce bulunan Babil metodu ile bulalım.
ilk önce X0 (0 ‘dan büyük rastgele bir sayı) gibi bir başlangıç değeri seçelim. Bu sayı 1, 5, 7, 40 gibi istenilen bir sayı olabilir. Ancak √7 ‘nin değerine ne kadar uzaksa sonucu bulmamız o kadar uzun sürecektir.
Başlangıç değerimizi X0 = 1 alalım. n = 0, 1, 2, … diye değerimizi bulana kadar devam edelim.
√7 sayımızın hesap makinesindeki değerini bulduk. Peki doğru değeri bulduğumuzu nasıl anlarız?
Algoritma √7 sayısındaki X5 değeri gibi belli bir değerden sonra hep aynı sayıyı tekrar etmektedir.
4 => 2,875 => 2,654891 => 2,645767 => 2,645751 => 2,645751 =>…
Zaten 2,645751 olarak bulduğumuz bu değerin karesini aldığımızda sonuç 7 çıkıyor.
( 2,645751 )2 = 7
Peki başlangıç değerini √7 ‘den küçük olduğunu bildiğimiz 1 yerine √7 ‘den büyük olduğunu bildiğimiz 40 sayısını seçsek sıralama nasıl olurdu?
40 => 20,0875 => 10,21799 => 5,451527 => 3,367785 => 2,723151 => 2,646851 => 2,645752 => 2,645751 => 2,645751 => …
Görüldüğü gibi işlem uzuyor ama yine aynı değer bulunuyor. Bu yöntemle ( – ) değere sahip sayılarında karekökünün olmadığı görünüyor. Mesela -1 sayısının karekökünü bulmaya çalışalım.
Başlangıç noktamızı X0 = 2 seçelim.
0,75 => 1,568452 => 0,465441 => -0,84153 => 0,17339 => …
Görüldüğü gibi sabit bir değere doğru yaklaşmıyor ve belli bir düzene göre artmıyor veya azalmıyor.
Peki Bu Yöntem Bize Nasıl Oluyor da Doğru Sonucu Veriyor?
Köklü Sayıları Nasıl Hesaplıyoruz?
Başlangıçta bir X0 değeri seçiyorduk. Rastgele seçtiğimiz bu değer köklü ifademizden büyük veya küçük bir değer oluyordu. İki durumu da sırayla inceleyelim. Seçtiğimiz bu değer ilk başta köklü ifademizin asıl değerinden küçük olsun.
X0 < √7
Eşitliğimizin her iki tarafı da X0.√7 ‘ye bölündüğünde;
Eşitsizliğin her iki tarafını da 7 ile çarpalım.
Başlangıçta X0 yani başlangıç noktamızın √7 irrasyonel sayısından küçük olduğunu kabul etmiştik. Bu durumda yeni eşitsizliğimiz;
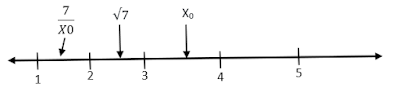
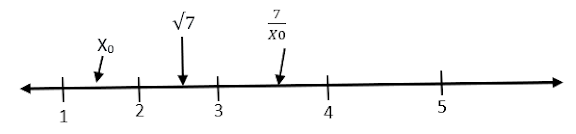
olur. Bu durumda √7 sayısı sayı doğrusunda;
Bu şekilde devam ederek gerçek değeri buluyoruz.
Peki başlangıçta seçtiğimiz sayı √7 ‘nin değerinden büyük olduğunda doğru sonuç nasıl çıkıyor?
Her iki taraf X0 . √7 ‘ye bölündüğünde;
Olur. Her iki tarafta 7 ile çarpıldığında;
buluruz. Başlangıç değerimizin √7 sayısından büyük olduğunu kabul etmiştik. Bu durumda yeni eşitliğimiz;
Aynı şekilde bu iki sayının ortalaması alındığında √7 sayısına iki sayıdan da daha yakın bir sayı ortaya çıkıyor.
Başlangıç noktamız √7 ‘nin tam değeri olduğunda;
olacağından ortalaması da aynı değeri verecektir.
Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.